뭣이 중헌디 ! 특성의 중요도
Feature Importance, Permutation Importance, PDP, SHAP
단일 모델일 때는 상대적으로 모델이 왜 이러한 결과를 내었는가 알기 어렵지 않았습니다. Tree 모델에서는 Feature가 얼마나 잘 나누는가에 따라서 그 중요도를 나타낼 수 있었고, 선형회귀모델은 각 회귀변수를 통해서 얼마나 영향을 미치는지 알 수 있었습니다. 그래서 결과를 이해하고 설명하는데 문제가 없었습니다. 하지만 앙상블기법과 같이 여러 모델을 합치는 등, 모델이 점점 복잡해지면서 그 중요도를 나타내는데 무리가 있었습니다. 그러나 문제가 무언지 알면 항상 해결해왔듯이 여러 방법이 등장하였습니다. 이번 포스트에서는 그 중요도를 나타내고자 몇가지 방법을 소개합니다.
Feature Importance
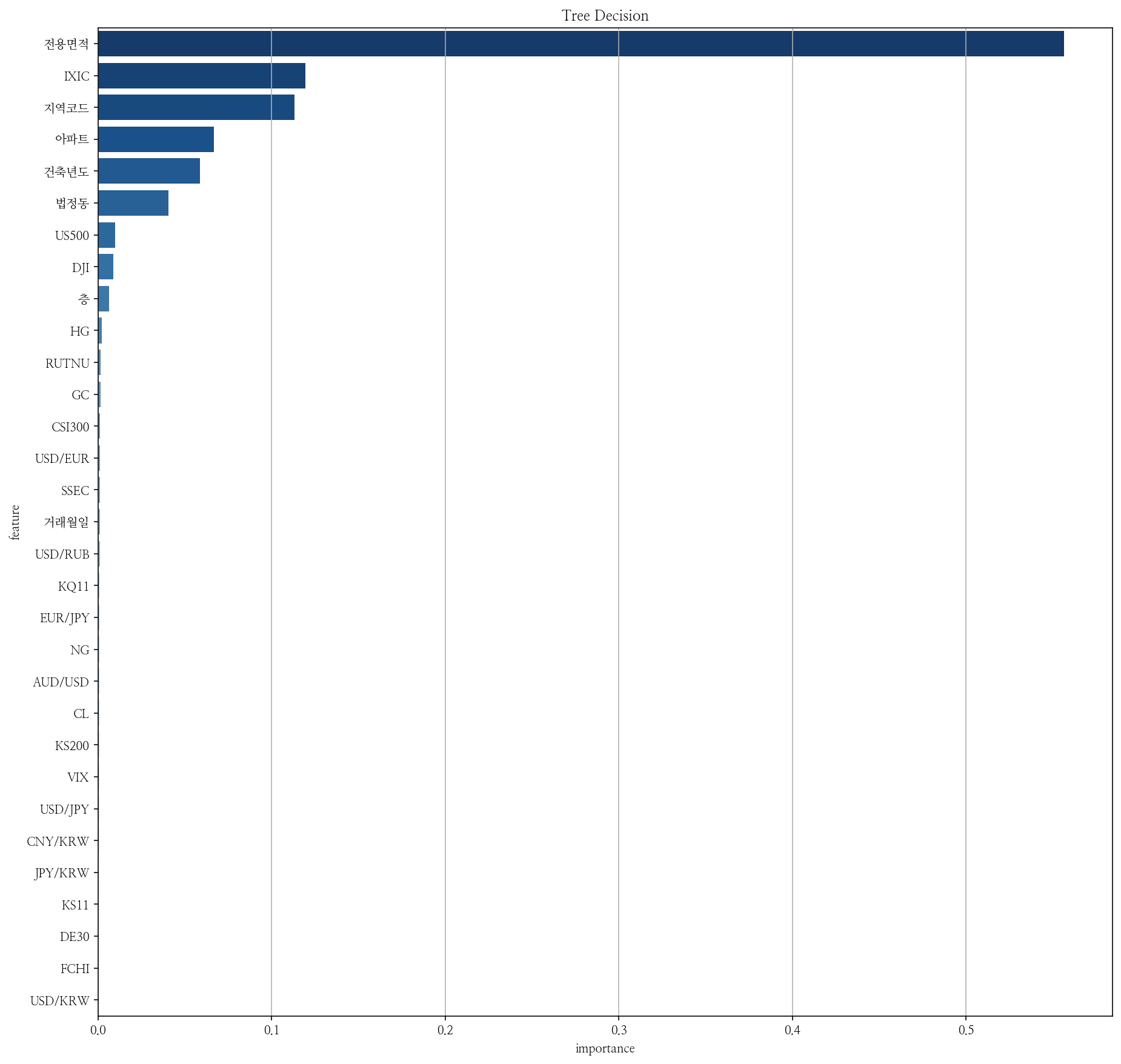
앞서 말했듯이 트리기반모델은 Feature가 얼마나 잘 나누는가에따라서 중요도를 알 수 있었습니다. 가장 간편하고 쉽고 직관적입니다. 다만 어떻게 영향을 미치는지는 알 수 없었습니다. 모델을 fit한 것을 기반으로 나타내므로, 예측 시에 데이터마다 어떻게 영향을 미치는지 알기 힘들었습니다. 또한 새로운 데이터가 나올 때마다 새롭게 fit해야 하므로 시간이 오래걸린다는 단점이 있었습니다.
zipp = []
for zipper in zip(X_train.columns, pipe.named_steps['decisiontreeregressor'].feature_importances_):
zipp.append(zipper)
zipp = pd.DataFrame(zipp,columns=['feature','importance']).sort_values('importance',ascending=False)
plt.figure(figsize=(15, 15))
sns.barplot(y = zipp.feature, x= zipp.importance, palette='Blues_r')
plt.title("Tree Decision");
Permutation Importance


위의 단점을 보완하기 위해서 이미 fit이 된 모델을 사용하여 predict하면서 특성의 중요도를 뽑습니다.
비교하기 위해서는 다른 것은 고정시키고 하나만 바꿔야합니다. 과정은 다음과 같습니다.
비교할 Feature하나를 뽑습니다. 그리고 한 Feature만 랜덤하게 섞습니다. 비율은 유지한채로요. 그리고 예측해봅니다. 예측값들이 어떻게 변하는지에따라 중요도를 산출합니다.
예를들어, A라는 특성의 중요도를 계산해봅시다. 데이터별로 100, 200, 200, 300, 300이 있습니다. 이를 랜덤하게 섞어줍니다. 그리고 타겟을 예측합니다. B와 C,D도 같은 방법으로 반복합니다. 그리고 이들을 비교합니다.
만약, 한 Feature를 섞었는데 드라마틱한 변화가 있다면, 그 특성은 중요한 특성이라는 의미겠죠?
반면에 한 Feautre를 섞어도 변화가 거의 없다면, 그 특성은 예측하는데 영향을 많이 미치지 못한다는 의미로 중요성이 떨어진다고 할 수 있습니다.
특성이 '얼마나'영향을 미치는지 알 수 있었습니다. 다만, 특성이 '어떻게'영향을 미치는지는 알 수가 없었습니다.
zipp = []
for zipper in zip(X_train.columns, permuter.feature_importances_):
zipp.append(zipper)
zipp = pd.DataFrame(zipp,columns=['feature','importance']).sort_values('importance',ascending=False)
plt.figure(figsize=(10, 8))
sns.barplot(y = zipp.feature, x= zipp.importance)
plt.title("Permutation Importance",fontsize=20);
PDP & SHAP
Permutation까지 이해하셨다면, PDP와 Shap은 어렵게 느껴지시지 않을겁니다. pdp와 shap의 개념이 헷갈리지 않기위해 함께보도록 하겠습니다.
PDP(Partial Dependence Plot) 특성하나가 전체 target의 평균에 미치는 영향 (ice curve의 평균)
ICE curve(Individual Conditional Expectation) 특성하나가 각 관측치의 타겟에 미치는 영향
SHAP (Global) 특성 전체가 target 전체에 미치는 영향
SHAP (Local) 특성 전체가 각 관측치의 타겟에 미치는 영향
__________________________________________________________________________________________________________
PDP

Permutation은 값을 랜덤하게 섞었다면 PDP는 다 똑같은 값을 넣음으로써 어떻게 영향을 미치는지 나타냅니다.
먼저 퍼센타일(백분위수,percentile)로 나눈뒤에 Grid Point를 잡습니다.
예를들어, Feature A가 있고 퍼센타일로 나누었을 때 Grid Point를 5로 잡는다면, feature 데이터의 0%,25%, 50%, 75%,100%에 해당하는 값이 Grid Point가 될 것입니다.
이제 Feautre A를 모두 첫번째 Grid Point로 바꿉니다. 그리고 예측값의 평균을 냅니다.
이제 Feautre A를 모두 두번째 Grid Point로 바꿉니다. 그리고 예측값의 평균을 냅니다.
이제 Feautre A를 모두 세번째 Grid Point로 바꿉니다. 그리고 예측값의 평균을 냅니다.
이제 Feautre A를 모두 세번째 Grid Point로 바꿉니다. 그리고 예측값의 평균을 냅니다.
Grid Point에 따라서 예측값의 평균이 달라지는 것을 볼 수 있습니다. 다시말하면, Feature A가 예측하는데 있어 어떻게 영향을 미치는 지 알 수 있습니다.
위 그림은 전용면적에 따른 집값 예측을 나타낸 PDP입니다. 전용면적(가로축)이 커지면 커질 수록 집값(세로축)이 커지는 것을 확인할 수 있었습니다.
ICE curve
각 관측치에 미치는 영향을 알고싶으면 관측치하나만 빼서 보면 되겠죠? 위의 PDP예시그림에서 파란선이 사실 각 개별치의 ICE curve입니다. PDP는 이들의 평균선이 되는 것이구요
ICE-PDP를 시각화한 gif입니다. twitter.com/i/status/1066398522608635904
Interact


Feature 2개를 함께 볼 수도 있습니다. 전용면적에대한 PDP가 하나, 건축년도에대한 PDP가 하나, 이 둘을 합쳐 Heatmap으로 표현할 수도 있고, 3D를 통해 출력할 수도 있습니다. 특성끼리 상호작용하는 것을 확인할 수 있겠죠
SHAP
게임이론을 바탕으로하는 SHAP은 크게 두가지로 나눌 수 있습니다.
전체데이터(의 일부)를 가지고 특성의 형향력을 알아보는 방법(Global)과
개별데이터를 가지고 각 데이터에 특성이 어떻게 영향을 미쳤는지 알아보는 방법(Local)이 있습니다.
Summary Plot

import shap
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X_train.iloc[10000:10500])
shap.summary_plot(shap_values, X_test.iloc[10000:10500])summary plot은 개략적으로 각 특성이 데이터에 어떤 영향을 미쳤는지 확인합니다. 점 하나하나는 각각의 데이터에 영향을 미친 정도입니다. 전체적으로 보면 위로갈 수록 평균적으로 크게 영향을 미친 것이고, 아래로내려갈 수록 작습니다.


# compute SHAP values
explainer2 = shap.Explainer(model, X_train_encoded.iloc[10000:10500])
shap_values2 = explainer2(X_test_encoded.iloc[10000:10500])
shap.plots.heatmap(shap_values2)instances는 각 데이터를 의미합니다. 이해가 쉽도록 히트맵을 2개 나누어보았습니다.
세로로 한줄한줄이 데이터 하나를 의미합니다. 데이터 하나하나 feature가 영향을 어떻게 미쳤는지 알 수 있습니다.
그리고 이를 모으면, 대채적으로 어떻게 영향을 미쳤는지도 확인이 되겠죠. 예를 들어 오른쪽 500개의 데이터를 시각화한 것을 보면, cluster라는 feature은 대체적으로 타겟의 값을 낮추는 역할을 했다고 해석할 수 있습니다.
Bar(Global)

# Bar형태로 표현 (Global)
shap.plots.bar(shap_values2)데이터 전체에 어떻게 영향을 미쳤는지 한눈에 확인할 수 있습니다.
x축은 Shap value의 평균입니다.

force_plot을 사용하면 자바스크립트를 이용해 좀 더 자세하게 볼 수 있습니다.
x축과 y축을 바꿔 특성하나하나별로 볼 수도 있고, 상호작용도 파악할 수 있습니다.
Bar (Local)

# Bar형태로 표현 (Local)
shap.plots.bar(shap_values2[15])데이터 하나를 뽑아서 시각화하면 위와같은 결과가 나옵니다.
데이터 하나에 어떻게 영향을 미쳤는지 한눈에 확인할 수 있습니다.
위의 경우는 IXIC라는 특성이 타겟값을 높였고,
size라는 특성이 타겟값을 낮췄네요.
다른 관측치를 뽑아봤습니다.

foce_plot을 사용하면 위와같이 시각할 수도있습니다. 예측값이 105,110.06이 나왔고, 각 특성이 영향을 미친 정도를 색깔과 바를 이용해 표현합니다.
* 분류문제일 때 음수값이 나오거나 0~1사이를 벗어나는 이유?
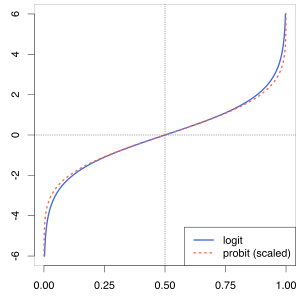
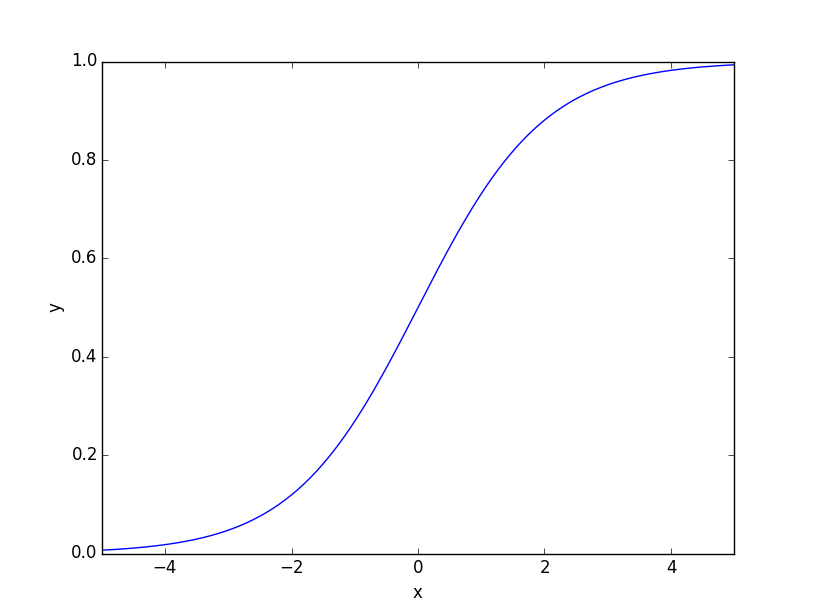
확률로 분류하는데 영향이 0~1사이를 벗어나거나 음수로 나오는 이유는 logit으로 계산하기 때문입니다. 이를 0과 1사이로 바꾸어 주려면, link = 'logit' 이라는 파라미터를 입력해주면 됩니다. 위의 왼쪽그림(Logit)에서 오른쪽으로 (Sigmoid) 바꿔주는거죠.
그러면 0과 1사이의 값으로 확인할 수 있습니다.
'인공지능 > 앙상블' 카테고리의 다른 글
| [Ensemble] Light GBM, 마이크로소프트의 부스팅 (0) | 2021.02.14 |
|---|---|
| [Ensemble] XGBoost, 극한의 가성비 (2) | 2021.02.14 |
| [Ensemble] Gradient Boosting, 차근차근 (0) | 2021.02.12 |
| [Ensemble] Ada Boost, 모델의 오답노트 (0) | 2021.02.11 |
| [Ensemble] 랜덤 포레스트, 나무가 이루는 숲 (0) | 2021.02.11 |




댓글