
추론의 방법
통계적 추론(statistical inference) 또는 통계적 추측은 모집단에 대한 어떤 미지의 양상을 알기 위해 통계학을 이용하여 추측하는 과정을 지칭한다. 통계학의 한 부분으로서 추론 통계학이라고 불린다. 추론 통계에는 도수 확률(frequency probability)과 사전 확률(prior probability)을 기반으로 하는베이즈 추론의 두 학파가 있다. - wikipedia
어떠한 모집단의 특성을 알고싶을 때는 그 집단을 조사하야합니다. 그런데 만약 모집단이 대한민국국민이라면 어떨까요? 아니면 아시아 전체에대해서 알고싶을 때는 어떨까요? 돈이 너무 많이든다, 시간이 많이 소모된다와 같은 너무나도 현실적인 이유로 접근자체가 힘들 수 있는데요, 이럴 때 우리는 '추론'을 합니다.
어떻게 추론을 할까요? 추론의 방법에는 크게 두가지가 있습니다. 일어난 횟수를 이용한 빈도확률을 이용한 방법을 사용하거나 확률을 미리 정해놓고 데이터를 수집해가며 그 정확성을 늘리는 사전확률과 사후확률을 사용하는 방법이 있습니다.
빈도확률 frequency probability
vs 사전확률과 사후확률 Prior probability & Posterior probability
Frequentist probability or frequentism is an interpretation of probability. it defines an event's probability as the limit of its relative frequency in many trials.
In Bayesian statistical inference, a prior probability distribution, often simply called the prior, of an uncertain quantity is the probability distribution that would express one's beliefs about this quantity before some evidence is taken into account.
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assignedafter the relevant evidence or background is taken into account.
앞서 말했듯이 빈도확률은 일어난 횟수를 가지고 추론하는 방법의 도구입니다. 예를 들어, 동전을 튕겨볼게요. 처음에는 앞면이 나오고, 두번째도 앞면 나왔습니다. 여기까지만보면 이 동전은 앞면만나오는 동전인 것 같습니다. 하지만 이를 수백번, 수천번 던져보면 결국에는 앞면과 뒷면이 나온 비율이 50:50으로 수렴하게 될 것입니다. 동전의 앞면을 0, 뒷면을 1로 나타내면 평균은 0.5가 되겠네요. 빈도를 통해서 확률을 나타내는 방법입니다.
만약 새로운 전염병에 대해서 전염률을 어떻게 알 수 있을까요? 사람을 대상으로 실험하면 되지 않을까요? 이를 수백번, 수천번 실험하면 우리는 원하는 결과를 얻을 수 있을 것 입니다. 하지만 이는 현실적으로 불가능합니다. 실제 사람을 대상으로 실험하는 잔인한 일은 할 수 없으니까요. 그럼 어떻게 알 수 있을까요? 우리는 먼저 사전확률(prior)을 정합니다. 기존의 여러 데이터를 통해 최대한 정확하게 정해봅니다. 다른 질병이라던지, 비슷한 단백질 구조를 가진 바이러스라던지 여러 방법이 있겠죠. 이렇게 정한 수치는 당연히 정확하지 않을 것입니다. 사전확률은 경험에 기반하며 불확실성을 내포하는 수치입니다.
환자가 늘어날 수록 데이터가 쌓입니다. 새로운 데이터를 통해서 이전에 정해놨던 사전확률을 업데이트 시킵니다! 이를 사후확률(posterior)이라고 합니다. 우리가 처음 정했던 확률은 데이터가 늘어날 수록 계속 업데이트되고 점점 더 정밀해 질 것입니다. 그 데이터가 많아질 수록, 시간이 더 흐를 수록 정교한 결과를 만들어 낼 것입니다!
빈도확률을 연역적인 추론이라고 할 수 있고, 베이즈 정리를 이용한 확률은 귀납적인 추론이라고 할 수 있습니다. 이것이 중요한 이유는 더이상 어떤 확률을 구하고자할 때 모든 표본을 조사한 뒤에 결과를 낼 필요가 없다는 뜻 입니다. 다시말해 데이터가 넘치는 지금 세상에서 보다 효과적으로 원하는 결과를 도출할 수 있다는 말이 됩니다.
조건부확률 Conditional Probability
In probability theory, conditional probability is a measure of the probability of
an event occurring, given that another event (by assumption, presumption,
assertion or evidence) has already occurred.

조건부 확률은 말그대로 어떤 조건이 주어지고 그에 따른 확률을 이야기합니다. 가령 A와 B가 있을 때, B가 일어난 상태에서 A일 확률을 뜻합니다. 수식으로는 위와 같이 씁니다.
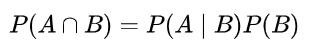
양변에 B인 확률인 P(B)을 양변에 곱하면 위와같은 식이 도출됩니다. 이를 곱셈공식이라고합니다. B인 조건에 A인 확률과 B의 확률을 곱하면 A와 B의 교집합, 즉 전체에서 A와 동시에 B인 확률이 도출됩니다.
예를들어 어떤 회사의 남자직원 중 30%가 헬스장에 등록했다고 하면 P(헬스장|남자직원) = 0.3이 됩니다. 만약 회사의 남녀 비율이 3:2라고 했을 때, 전체 직원 중 남자일 확률은 0.6입니다. 이 두가지를 곱하면 0.18, 즉 전체직원 중 남자직원이면서 헬스장에 등록한 직원일 확률은 0.18이 됨을 알 수 있습니다.
이제 아래 그림을 이해할 수 있습니다. 전체 집합은 A와 A가 아닌 것으로 나뉘고, A는 A이면서 B인것, A이면서 B가 아닌 것으로 나뉠 수 있습니다. 이 개념은 아래 전확률정리에서 중요한 내용이므로 잘 생각해보면 좋습니다.
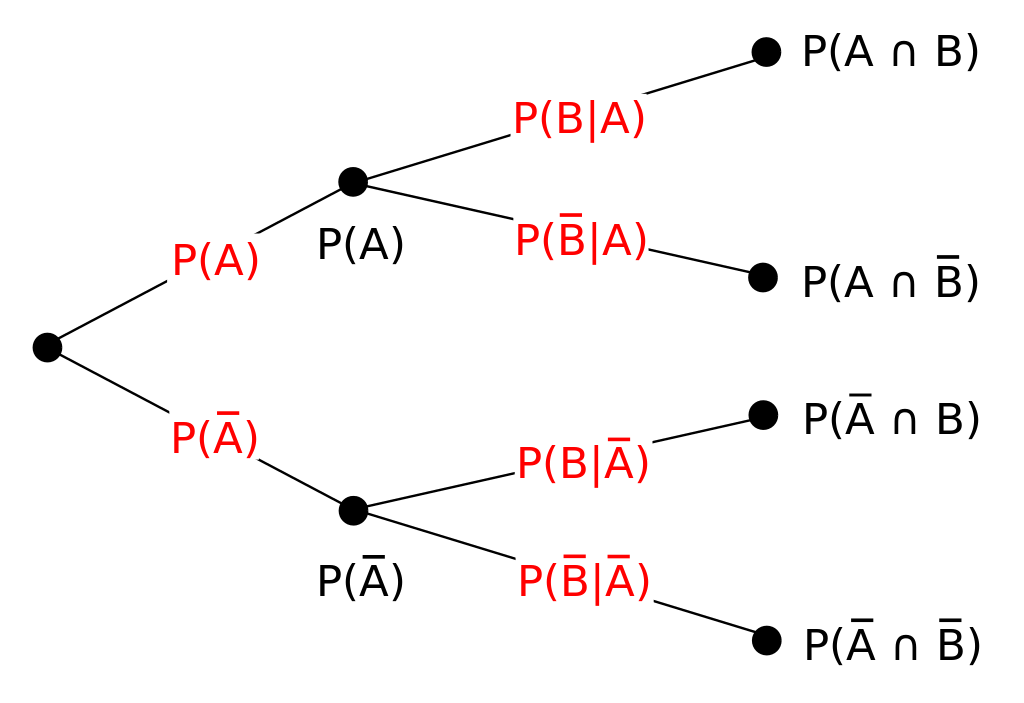
전확률정리 Law of Total Probability
In probability theory, the law (or formula) of total probability is a fundamental rule relating marginal probabilities to
conditional probabilities. It expresses the total probability of an outcome which can be realized via several distinct events—hence the name.
-wikipedia

전체를 S라고하고 B1,B2,...Bn 등으로 나누어 놓았을 때 (서로 겹치지 않게), A인 확률은 A이면서 B1일확률,A이면서 B2일 확률 ,...A이면서 Bn일확률을 모두 더한 것과 같습니다.

어떤 집합 A를 구하는 경우, 각 원인에 대한 조건부확률 P(A|Bi)와 P(Bi)의 곱에의한 가중합으로 구할 수 있다는 말입니다. 다시말해서 B와 A의 교집합인 확률을 모두 더하면 A의 확률을 구할 수 있는 것입니다 !
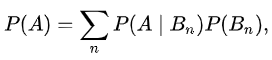
그럼 조건부 정리에서 도출했던 식을 보겠습니다. A와 B의 교집합은 (B이면서 A인 확률 X B의 확률)과 같다고 했습니다. 우리는 이제 전체를 B개로 쪼갠 뒤에 B에있는 A의 확률을 알아낼 수 있고, 알아낸 모든 확률을 더함으로서 몰랐던 A의 확률을 구할 수 있는 것입니다!
TP,TN,FP,FN

아무리 정밀한 진단 키트가 있다고 해도 그 키트는 100%로 양성과 음성을 구분할 수는 없을 것입니다. 매우 높은 확률이라도 분명 잘못된 진단을 할 수 있습니다. 위그림은 이를 나타내주는 그림입니다.
왼쪽의 어두운 부분은 보균자인 집단이고, 오른쪽은 보균자가 아닌 집단입니다. 원안에 있는 집단은 진단키트가 양성이라고 판단한 영역입니다. 초록색(true positives)은 실제 보균자를 양성으로 판단한 것이고, 빨간색(false positive)은 실제 보균자가 아닌데 양성이라고 판단한 것입니다.
이를 표로나타내면 아래와같습니다. 이를 혼동행렬, Confusion Matrix라고 합니다.


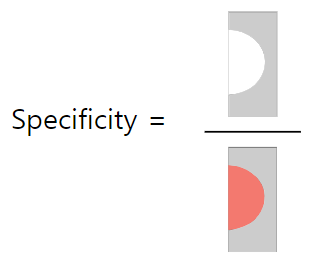
키트가 얼마나 정확한지 어떻게 알 수 있을까요? 우리는 그래서 민감도(Sensitivity)와 특이도(Specificity)의 값을 구합니다. 진단의 관점에서 민감도란 보균자를 양성으로 판단하는 정도입니다. 즉 진짜를 진짜라고 잘 찾아내는 정도입니다. 특이도는 보균자가 아닌사람을 음성이라고 판단하는 정도입니다. 다시말해 정상인사람을 정상이라고 잘 찾아내는 정도입니다. Sensitivity는 TPR(True positive rate)이라고도 쓰이며 'TP/ P'입니다. Specificity는 TNR(True negative rate)이라고도 쓰이며 'TN/N'입니다.
우리는 이제 TPR과 TNR을 통해서 베이지안 추론을 사용할 수 있습니다.
베이즈정리 Bayes' Theorem
In probability theory and statistics, Bayes' theorem (alternatively Bayes' law or Bayes' rule), named after Reverend Thomas Bayes, describes the probability of an event, based on prior knowledge of conditions that might be related to the event. -Joyce, James (2003), "Bayes' Theorem"

핵심은 사전확률을 지속적으로 업데이트한다는 데 있습니다. 전확률 정리에서 우리는 B집단에 속한 A의 확률을 가중합으로 A를 구할 수 있었습니다. 베이즈 정리에서 가장 헷갈리는 것은 사전확률과 사후확률일텐데요, 사전확률은 P(A)이고 사후확률은 P(A|B)입니다.
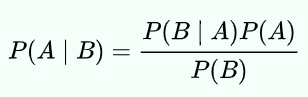
베이즈 정리는 사전확률(P(A))를 가지고 있다가 새로운 데이터가 들어오면 그 데이터를 이용해서 사후확률(P(A|B))를 도출하여 사전확률과 사후확률의 관계를 설명하는 확률입니다.
우리가 조건부확률과 전확률의 정리를 통해 아래와 같이 표현할 수 있습니다. 우리는 A와 B의교집합 = P(B|A)P(A) 임을 알고있다. 또 우리는 A와 B의교집합 = P(B|A)P(B)임을알고있다.
즉, A와 B의교집합 = P(B|A)P(B) = P(B|A)P(A) 가된다.
P(B|A)P(B) = P(B|A)P(A) 여기서 P(B)로 나눈다면?! 위와 같은 식을 볼 수 있다! 아래에서 다시보자!
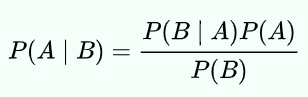
다시 P(B)는 조건부확률에서 봤듯이, B이면서 A일 확률과 B이면서 A가 아닐 확률과 같다. 즉! 그리고 이것은
조건부 확률에서 A와 B의교집합 = P(B|A)P(A)가 되고 B이면서 A가 아닌 것도 마찬가지로 되서 아래와 같은 식이된다!
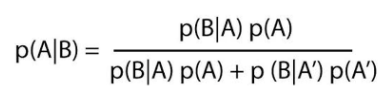
예제 1

실제로구해봅시다.
신문기사를 보니 음주운전을 하는 사람은 전체인구에서 0.5%라고한다. 음주테스트 기계는 99%의 민감도로 실제 음주했을 때 양성반응을 보이고, 90%의 특이도로 음성일때 음성반응을 보인다.
음주테스트를 했는데 양성이 나왔다. 이 사람이 실제로 음주운전을 했을 확률은 얼마나 되는가?
Hypothesis: 음주운전을 했다.
Evidence: 양성반응이 나왔다.
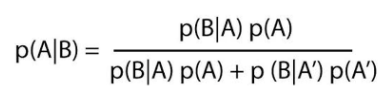
P(A) = 0.5% Hypothesis, 실제 음주운전을 하는 사람들의 비율
P(B|A) = 99% True Positive
P(B'|A') = 90% True Negative
이를 계산하면
p(B|A)p(A) = 0.99 x 0.005
p(B|A)p(A) + p(B|A')p(A') = 0.99 x 0.005 + 0.1 x 0.995
값은 0.04786979415, 즉 4.7%에 근사하게 됩니다.
음주운전을 걸린 사람이 실제로 음주운전을 했을 확률은 4.7%가 됩니다. 너무낮다고?
예제2
그럼 한번만 검사해서는 이사람이 진짜 술을 마셨는지 모르겠죠. 만약 양성인 사람들에게 또 검사를 한다면 어떨까요?
앞에서 구한 값이 사전확률이 됩니다. 즉 P(A)는 0.04786979415로 업데이트 된것입니다. 가설이 달라집니다.
Hypothesis: 양성이 나왔고 이는 사실이다.
앞에서 구한 4.7%으로 사전확률값이 갱신되었습니다. 우리는 우리의 가설이 맞는지 검정할 수 있습니다.
똑같은 방식으로 계산했을 때 38.59%에 근사한 값을 구할 수 있습니다. 이 값으로 또 할 수 있겠죠?
1 회차 : 4.79%
2 회차 : 38.59%
3 회차 : 88.71%
4 회차 : 98.99%
5 회차 : 99.92%
6 회차 : 99.99%
4회차부터 이미 99%에 근사한 것을 확인할 수 있습니다.
'기본소양 > 통계' 카테고리의 다른 글
| [ 통계, 처음입니다] 헷갈리는 양측검정, 단측검정 (one-tailed, two-tailed) (0) | 2021.01.06 |
|---|---|
| [통계, 처음입니다] 가설검정 (귀무가설과 대립가설, p-value) (3) | 2021.01.05 |
| [통계, 처음입니다] 들어가며, 샘플링(표본추출) (0) | 2021.01.05 |



댓글