행렬은 벡터를 변화시킨다
3Blue1Brown - Essence of linear algebra
원래 벡터의 정의부터 선형의 개념(결합과 생성, 종속과 독립 등)을 포함하여 포스팅 하려 글을 쓰고 있었으나, 너무 길어지고 파고들면 끝도 없어 압축하여 간단히 기억할 부분만 포스팅합니다. 강의를 수강하고 되돌아 보기위한 데 그 목적이 있습니다.
본 포스팅은 3blue1brown의 Essence of linear algebra를 시청하고 그 자료를 바탕으로 만들어진 자료입니다.
3Blue1Brown
3Blue1Brown, by Grant Sanderson, is some combination of math and entertainment, depending on your disposition. The goal is for explanations to be driven by animations and for difficult problems to be made simple with changes in perspective. For more inform
www.youtube.com
벡터의 합
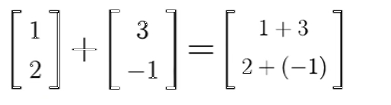
벡터와 스칼라의 곱
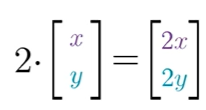
벡터와 스칼라를 곱해 선으로 표현 가능 >> LINE
벡터와 벡터를 더해 면으로 표현가능 >> SPAN
Real coordinate space
R^2에서 두 벡터의 합으로 모든 부분을 표현할 수 있습니다.
벡터의 모든 끝점의 집합이 두 벡터의 Span입니다. (span과 basis에 대해서는 다음 포스트에서 다룹니다.)
선형종속
벡터의 방향이 같다면 둘이 아무리 더해도 span으로 표현되지 않습니다 >> Linearly Dependent
선형독립
벡터의 방향이 다를 때 둘이 더하면 span이 됩니다>>Linearly Independent
기저 Basis
공간의 기저(basis)는 선형독립적인 벡터들의 집합으로 스팬하면 그 공간이 됩니다.
단위벡터 unit
길이가 1인 벡터를 의미합니다.
만약, matrix가 어떤 함수 등에 의해 변환(특수한형태로 제한)되었을 떄 단위벡터만 안다면 어떻게 변했는지 알 수 있습니다. i hat, j hat으로 표기하고 값은 (1,0),(0,1)입니다. (3차원 k hat). 단위행렬이 결국 행렬에서 1을 의미하는데, i hat과 j hat, 이 둘을 의미하는 행렬입니다.
행렬과 벡터의 곱셈
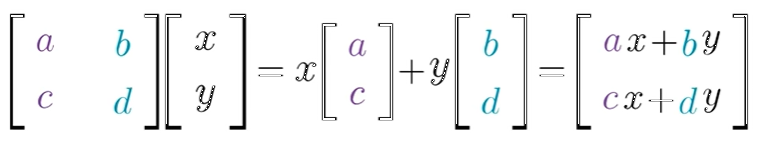
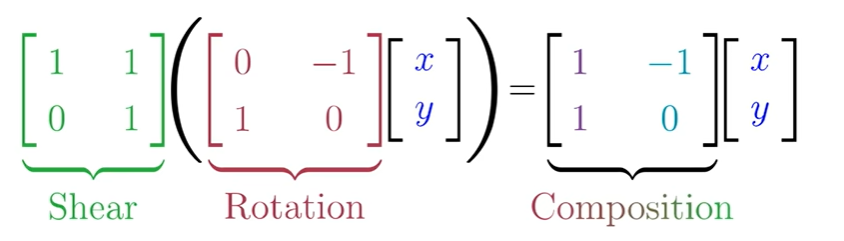
위에서 matrix가 어떤 함수등에 의해 변환 Transfromation되었다고 할 때, 이 것을 계산하는 방법입니다. 공간의 어떤 변환이라고 생각해야합니다. 기존의 i hat과 j hat으로 표기 되었던 모든 벡터가 행렬을 통해 공간이 변환되고, 우리는 i와 j가 어떻게 변했는지 알면 어떻게 변환되었는지 그 값을 계산할 수 있습니다. 위 식은 오른쪽에서 왼쪽으로 봐야합니다. 이는 함수표기와 닮았다고 생각하면 쉽습니다. 기호로 표기하면 다음과 같습니다.

x y 라는 벡터를 행렬을 Rotation시키고, Shear시키는 것. 행렬은 연산자의 역할을 합니다.
오늘 포스팅의 제목입니다. 행렬은 벡터를 변화시킨다!
행렬식



만약 벡터사이의 넓이가 A라고했을 때 위와같은 행렬을 곱하게되면, 넓이는 6A이 됩니다. 다시말해 6배넓어지는 것. 선형변화에 의한 영역의 변화를 나타내는 것입니다. 이를 determinant라고 부릅니다.
우리가 ad-bc라고 고등학교때 배웠던 그것입니다.

위그림은 determinant가 4,2로 2,1로가니까 같은방향의 벡터로 향하게되고, 선형으로 겹칩니다. 다시말해 모든 공간이 겹쳐서 선으로 되는 것입니다. 만약 영행렬인경우, 선이아니라 0인 원점으로 모든 공간이 겹쳐지게 됩니다.(차원이 축소되는 것) 음수인 경우는 뒤집혀진 것입니다.
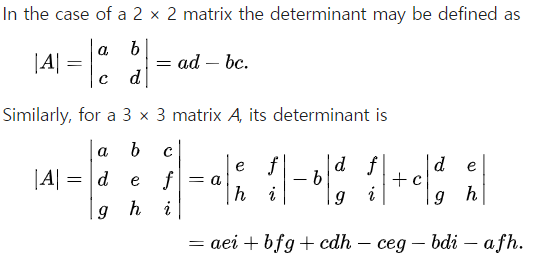

랭크 Rank
행렬로 인한 결과가 차원이 선이되면 Rank = 1, 면이되면 Rank = 2가 됩니다. 2x2 행렬은 최대랭크가 2입니다. 원점으로 이동할 때 이동되는 벡터의 집합을 그 행렬의 영공간(Null space)혹은 커널(Kernel)이라고 부릅니다.
역행렬 Inverse
더낮은 차원으로 변환하는 행렬이 아닌 한 ( det가 0이 아닌 한) 단위행렬로 돌아올 수 있는 역행렬이 존재합니다. 꼬여있던 형태를 다시 원래대로 복구시키는 행렬이 됩니다.
쉽게말해 A 와 A-1을 곱하면 단위행렬이 됩니다.
벡터의 내적 (Dot product)


v와 w를 내적할 경우, v에 w를 투영 project해서 투영된 w의 길이와 w의 길이를 곱하는 것.
이는 서로 투영시켜도 같은 값이 나오기 때문에 교환법칙 성립함.
수직으로 투영시킨 값이기 때문에 norm값에 코사인 각도를 곱해주는 것
값은 스칼라입니다.
벡터의 외적 (Cross product)

v와 w간의 면적을 구하는 것. 앞서 행렬식 determinent의 개념이 필요합니다. 우리는 단위벡터를 행렬을 통해 변형시켜주는 것입니다. i hat과 j hat의 면적은 1입니다. v와 w를 행렬로 만들고, determinent를 구해주면 그 넓이를 구할 수 있습니다.
외적은 차원을 높이는데 중요한 역학을 합니다. v와 w의 곱으로 구한 넓이(평행사변형)의 값이 수직한 방향으로 p가 됩니다.
값은 벡터입니다.
'기본소양 > 선형대수학' 카테고리의 다른 글
| 파이썬으로 하는 선형대수학 (1. 스칼라와 벡터 & 2. 매트릭스) (0) | 2021.01.18 |
|---|---|
| [선형대수학] 차원을 왜 축소시키는가 (0) | 2021.01.15 |
| [선형대수학] 공분산과 상관계수 ( 피어슨, 스피어만) (0) | 2021.01.14 |
| [선형대수학] 고유값과 고유벡터, 벡터의 변환 (0) | 2021.01.14 |
| [선형대수학] 벡터의 차원 (0) | 2021.01.13 |




댓글