고유값과 고유벡터, 벡터의 변환
지난번 보단깊게, 그러나 너무 깊지 않게
앞 포스트와 이어집니다.
Eigenvalues
고유벡터와 고유값은 왜 알아야할까요?
우리는 행렬과 벡터를 곱하는 것을 배움으로써 선형변환(Linear transformation)을 알았고,
행렬식(Determinants)를 통해서 선형변화에 의한 영역의 변화를 알았고 (이를통해 span의 축소와 확장을 알았으며),
기저(Basis)가 변할 수 있다는 사실을 알았습니다.
행렬로써 우리는 좌표계를 바꾸고, 이는 기저를 바꿀 수도 있습니다.
이제 우리는 기저를 바꿀 것 입니다. 좌표계를 바꿔서 말이죠

잠깐 복습해 보겠습니다. 위 행렬의 의미는 무엇일까요? i hat(1,0)이 (5,2)로 이동하게하고, j hat(0,1)이 (2,4)로 이동하게하는 행렬의 의미입니다.
이제 본격적으로 고유벡터와 고유값을 통해 알아보겠습니다.
행렬을 통해서 좌표계를 바꿀 때 벡터는 그에따라 변하게됩니다.
하지만 바뀌지 않는 벡터도 존재합니다. 예를 들어 R^2에서 y=x로 선형변환을 시킬 떄, [1,1]이나 [2,2]는 변하지 않게되겠죠! R^3도 마찬가지로 어떤 축을 기준으로 변형을 시킵니다. 이때 축에있는 벡터들은 변하지가 않습니다. 이를 고유벡터라고합니다. 고유벡터를 알 수만 있다면 우리는 좌표계가 어떻게 변했는지 알 수 있습니다.

이렇게 표현합니다. A라는 행렬을 이용해서 v라는 고유벡터를 곱한 값은 람다(상수,scalar)라는 고유값을 곱한 값입니다. 다시말해 A라는 변형을 가했는데도 람다(scalar)라는 상수만 곱해줄 뿐, 벡터의 방향은 변하지 않는 거죠! 여기서 람다는 '고유값'입니다.
우리는 이 조건을 만족시키는 벡터와 람다를 찾고싶습니다. 이는 곧 변형을 가해도 변하지 않는 고유벡터와 고유 값이니까요.
하지만 상수랑 A랑 람다랑 같다는 것은 좀 이상하게 느껴집니다. 그래서 우리는 자기자신을 의미하는 단위행렬을 곱해줌으로써 계산할 수 있도록 만들어줍니다. 수식으로 표현하면 다음과 같습니다.

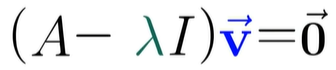
오른쪽 항에 있는 벡터를 좌항으로 넘기면 괄호로 묶을 수 있습니다.
그럼 곧 이 식은 v를 영벡터로 만들어 주기만 하면 되죠. 여기서 행렬식이 등장합니다.
영벡터를 만들어 준다는 것의 의미는 차원을 낮추는 것입니다. 다시말해 행렬식이 0이 되면 우리는 원하는 값을 얻을 수 있습니다.

행렬식을 통해서 고유 값이 무엇인지 알 수 있습니다.
Eigenvectors
이제 고유벡터를 구해보겠습니다.
우리는 행렬식을 이용해서 람다의 값을 구했습니다. v는 아직 모르니 [x, y]라고 두겠습니다.

이 조건의 x와 y를 만족하는 모든 벡터가 고유벡터가 됩니다. 선형이 되겠죠?

위 행렬을 보면 대각선에만 값이있고 나머지는 0입니다. 이런 형태를 대각선행렬(Diagonal matrix)이고 값만큼 크기만 확장하게됩니다. 스케일링한다는 말이죠! 다시말해 각 열은 '기저벡터'이면서 '고유벡터'이고 그 값은 '고유값'입니다.
추가
회전을하게되면 같아지는 벡터는 없습니다. 어떤 벡터도 같을 수 없습니다. 다시말해 회전을 하게 만드는 행렬은 어떤벡터도 같은 벡터로 있지 못하게합니다. 이때 고유값은 허수입니다. 회전행렬에대해서는 추후에 더 자세히 다루도록 하겠습니다.
'기본소양 > 선형대수학' 카테고리의 다른 글
| 파이썬으로 하는 선형대수학 (1. 스칼라와 벡터 & 2. 매트릭스) (0) | 2021.01.18 |
|---|---|
| [선형대수학] 차원을 왜 축소시키는가 (0) | 2021.01.15 |
| [선형대수학] 공분산과 상관계수 ( 피어슨, 스피어만) (0) | 2021.01.14 |
| [선형대수학] 벡터의 차원 (0) | 2021.01.13 |
| [선형대수학] 행렬은 벡터를 변화시킨다 (0) | 2021.01.12 |




댓글